Kapitalwert: Der Wert eines Angebots

Als Selbstständige wollen wir Angebote schaffen, die mehr wert sind als sie kosten.[1] In diesem Artikel geht es um uns als Käufer: Wie berechnen wir den Wert eines Angebots? Der Standard dafür ist der »Kapitalwert«. Er besagt, wie viel zukünftige Zahlungen heute wert sind. So können wir Risiken besser bewerten und prüfen, ob sich ein Geschäft für uns lohnt. Ich erkläre die Grundlagen des Kapitalwerts und zeige, wie Sie ihn am Beispiel einer Gym-Mitgliedschaft und einer Immobilie selber nutzen können.

In diesem Artikel geht es primär um das Rechnen. Qualitative Faktoren und fortgeschrittenere Risikoanalysen folgen in zukünftigen Artikeln.

Der Wert eines Angebots hängt davon ab, wann die Zahlungen erfolgen. Ein Beispiel:

• Szenario A: 5 Jahre lang spare ich je 1.000 EUR und im sechsten Jahr zusätzlich 5.000 EUR
• Szenario B: Im ersten Jahr spare ich 5.000 EUR und in den nächsten 5 Jahren je 1.000 EUR

Jeweils erhalte ich 2 % p. a. auf Sparguthaben. Jeweils spare ich 10.000 EUR. Trotzdem unterscheidet sich das Endvermögen:

Im Szenario B liegt mehr Geld länger auf dem Konto – und erzielt deshalb höhere Zinsen. Zeit ist beim Vermögensaufbau einer der entscheidenden Faktoren. Aber auch Inflation, Steuern, Abschreibungen oder Sonderzahlungen beeinflussen, wie viel ein Angebot tatsächlich wert ist. All das müssen wir einpreisen.

Mein Fitnessstudio bot mir an:

• monatlich 45 EUR, oder
• einmalig 2.500 EUR für eine lebenslange Mitgliedschaft

Lohnt sich die Einmalzahlung? Mein Gym argumentierte: Nach 4,5 Jahren hätte sich die Mitgliedschaft amortisiert:

Das stimmt aber nur, wenn ich mein Geld auf dem Sparbuch oder Girokonto versauern lasse und es keine Inflation gibt. Beides trifft bei mir nicht zu.

Beim Kapitalwert erstellen wir ein Modell, das ein Geschäft vernünftig auf unsere Lebensrealität abbildet.

Für die Berechnung des Kapitalwerts brauchen wir einen Referenzzins. Typische Quellen dafür sind:[2]

• Zinssätze auf 10-jährige deutsche Staatsanleihen
• die erwartete Inflationsrate
• Opportunitätskosten für alternative Investments
• eine Kombination daraus zzgl. Risikoaufschläge

Wenn ich die 2.500 EUR nicht für die lebenslange Mitgliedschaft verwende, würde ich das Geld in einen breitgestreuten ETF anlegen. Die langfristige, reale Rendite eines Weltportfolios wie den ACWI IMI beträgt im Mittel 7,5 % p. a.[3] »Reale Rendite« bedeutet: Die mittlere Inflation ist bereits abgezogen. Risikoaufschläge lassen wir für den Moment außer Acht.

Es macht finanziell keinen Unterschied, ob ich bei 7,5 % p. a. sofort 502,33 EUR zahlen ODER diesen Betrag spare und in einem Jahr 540 EUR zahle. Genau das ist der Kapitalwert: Der heutige Wert zukünftiger Zahlungen. Das veranschaulicht folgende Grafik:

Für 2 Jahre gilt dasselbe Prinzip. Wir müssen die zweiten 540 EUR nur über 2 Jahre abzinsen:

Analog gilt: Es macht keinen Unterschied, ob ich sofort 969,61 EUR zahle ODER 969,61 EUR zu 7,5 % p. a. spare und davon nächstes sowie übernächstes Jahr jeweils 540 EUR auszahle.

Den heutigen Wert der lebenslangen Mitgliedschaft berechnen wir analog. Ich zahle sofort 2.500 EUR und in jedem folgenden Jahr spare ich 540 EUR. Im Excel schön übersichtlich:

Ergebnis: Bei einem Zinssatz von 7,5 % p. a. hätte sich die lebenslange Mitgliedschaft nach 6 Jahren geradeso abbezahlt – also 1,5 Jahre oder ein Drittel länger, als mein Gym behauptet hat.

Alternativ können wir auch die Excel-Funktion XKAPITALWERT (oder in Google Sheets XNPV) verwenden. Für komplexere Analysen wie eine Monte-Carlo-Simulation sind die Zeilen 7 und 8 jedoch unverzichtbar.

Angenommen, ich komme tatsächlich in den Genuss einer lebenslangen Mitgliedschaft. Das bedeutet, dass ich jedes Jahr 540 EUR spare. Den Wert dieser unendlichen Zahlungen modellieren wir mit der sogenannten »ewigen Rente«:

Setzen wir die Werte ein:

und es ergibt sich für den Kapitalwert:

Das Gleiche im Excel:

In der Darstellung habe ich die ewige Rente auf Anfang des siebten Jahres beziehungsweise Ende des sechsten Jahres abgezinst. Das veranschaulicht folgende Abbildung.

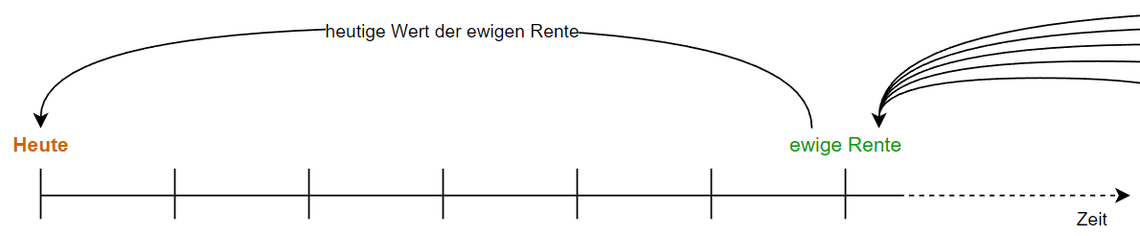
Bei konstanten Zinssätzen macht es keinen Unterschied, wann die ewige Rente angesetzt wird. Interessant wird es, wenn sich Zinssätze oder Wachstumsraten ändern. Angenommen, der Jahresbeitrag wächst alle drei Jahre um 5%:

Der Kapitalwert steigt nur geringfügig, da die höheren Beiträge weit in der Zukunft liegen. Dieses Risiko ist im Kapitalwert bereits berücksichtigt.

Der Charme der Methode: Oberhalb der Abzinsung können wir die Rechnung flexibel anpassen, z. B. mit Deckungsbeiträgen, Stückkosten, Mengen, Abschreibungen, Steuern, Kreditkosten, Wachstumsraten oder Inflation. Dazu ein Beispiel.

Eine Immobilie wird ohne Eigenkapital gekauft, vermietet und nach 10 Jahren steuerfrei verkauft:

Darin sind folgende Punkte berücksichtigt:

• Zeilen 5–6: Steuerwirksame Abschreibungen und Kreditzinsen
• Zeile 12: Steuerunwirksame Tilgung
• Zeilen 16–21: Kreditzinsen und Tilgung getrennt
• Zeilen 23–30: Steuerersparnis durch steuerliche Verluste
• Zeilen 33–36: Verkauf des Objekts und Kreditauslöse
• Zeilen 37–39: Kapitalwert

Das Beispiel zeigt auch: Aus buchhalterischen oder steuerlichen Gewinnen/ Verlusten können wir nicht den Wert eines Angebots ableiten. Der Kapitalwert hingegen liefert eine fundierte Entscheidungshilfe.

In Zeile 5 der Immobilienkalkulation ziehe ich die Abschreibung für Abnutzung (AfA) ab und in Zeile 11 addiere ich sie in gleicher Höhe wieder auf. Warum? AfA ist steuerlich relevant, real fließt aber kein Geld. Die Zahlung ist fiktiv. Ähnlich verhält es sich bei:

• Rückstellungen
• Rechnungsabgrenzungsposten
• latenten Steuern
• Goodwill
• verdeckten Einlagen/Entnahmen
• Neubewertungen von Bilanzposten
• kalkulatorischen Größen, z. B. Unternehmerlohn, Miete, Pauschalen

Cash is King: Im Kapitalwert berücksichtigen wir nur real fließende Ein- und Auszahlungen. Warum? Weil sie tatsächlich über unseren Erfolg oder Misserfolg entscheiden.

Weitere interessante Details aus der Immobilienkalkulation zeigen sich bei den üblichen Kennzahlen wie der »Brutto- und Nettomietrendite«:

Zugegeben, diese Kennzahlen wirken unattraktiv. Makler und FinFluencer nennen diese Werte häufig – allerdings meist nur für das erste Jahr. Das sagt kaum etwas über fremdfinanzierte Investments aus. Mit dem Modell erkenne ich jedoch, welches Risiko ich eingehe: 10 Jahre lang würde ich draufzahlen, und alles hängt vom hohen Verkaufserlös ab. Ob deutsche Immobilien im Preis steigen, ist aktuell (Stand: 12/2024) ungewiss.[4] Ein blindes Vertrauen in steigende Werte ist daher äußerst riskant.

Das ist symptomatisch: Viele Leute gehen aufgrund von Intransparenz und verkürzter Kennzahlen enorme Risiken ein. Als Investoren wollen wir Risiken kontrollieren. Dazu müssen wir zunächst die Zahlen in absoluten Euro beziffern und anschließend einen großzügigen Risikopuffer einbauen.

Der entscheidende Hebel ist der Zinssatz: Höhere Zinssätze führen zu größeren Nennern und damit zu niedrigeren Kapitalwerten. Dieses Vorsichtsprinzip resultiert in niedrigeren Kapitalwerten, wie die folgende Tabelle zeigt:

Der Risikoaufschlag auf den Zins enthält eine entscheidende Information: Wie sicher sind wir, dass diese Kalkulation realistisch ist? Je unsicherer wir sind, desto höher der Risikoaufschlag. Selbst bei einem Risikoaufschlag von 100 % bleibt der Kapitalwert positiv – ein starkes Argument für die lebenslange Mitgliedschaft.

Keine Methode löst alle Probleme, und auch der Kapitalwert hat seine Grenzen. Oft wird kritisiert, dass er auf Annahmen basiert und sensitiv auf den Zinssatz reagiert.[5] Diese Kritik ist dämlich. Jede Rechnung beruht auf Annahmen und ist sensitiv auf gewisse Parameter. Die Frage ist, ob wir uns das bewusst machen.

Das eröffnet eine andere Perspektive. Es sind die Dinge, die wir für wahr halten, aber real falsch sind, die uns Probleme bereiten.[5] Der Kapitalwert ist auch ein Denkwerkzeug. Meine Immo-Kalkulation habe ich einmal aufgebaut und verbessere sie stetig. Sie dokumentiert mein Lernen und wie ich über Immobilienrenditen nachdenke.

Aber Modell bleibt Modell. Sie vereinfachen die Welt. Die Zahlungen werden so nicht eintreten. Es ist nur eine Wert- und Risiko-Schätzung:

Der Kapitalwert gibt an, ob wir bei über-pessimistischen Annahmen unser Geld eher vermehren (Kapitalwert > 0) oder eher vernichten (Kapitalwert < 0).

Genau hier lauert ein Problem: Leider verwechselt immer wieder jemand das Bild mit der Landschaft und formt aus den Zahlen eine fixe Erwartung. Dann ist er enttäuscht, wenn das Geschäft schlechter läuft – selbst wenn wir nur weniger Gewinn machen. Aktieninvestoren können ein Lied davon singen. Der Kurs rauscht ab, wenn Gewinnprognosen unerfüllt sind.

Kapitalwert-Modelle taugen für stabilere Geschäfte wie:

• Gebührenmodelle
• Maschinen
• Anleihen
• Immobilien
• Versicherungen
• Solaranlagen
• PKW
• Konsumaktien
• etc.

Die Bürokratie und Gesetze dieser Geschäfte sind relativ träge und »stabilisieren« den Aussagengehalt unseres Modells. Anders sieht es bei hochdynamischen Geschäften, wie Startups, Erfindungen, Innovationen oder Wachstumsaktien (z. B. Tesla). Deren Dynamik können wir nicht vernünftig in so ein Modell packen. Erwartungen und Enttäuschungen sind vorprogrammiert. Die eigentliche Kritik richtet sich daher nicht gegen den Kapitalwert selbst, sondern gegen unseren Umgang damit.

Unter den vielen Finanzkennzahlen gibt uns der Kapitalwert die klarste Antwort: Lohnt sich ein Investment für mich – ja oder nein? Seine Stärke liegt darin, den Wert eines Angebots greifbar zu machen und Risiken zu beziffern. So können wir fundierter entscheiden als mit verkürzten Versprechungen.

Welche Erfahrungen haben Sie mit Investitionen gemacht? Hätten Sie mit dem Kapitalwert andere Entscheidungen getroffen? Ich bin gespannt auf Ihre Kommentare und Anregungen!

Ihr, Nico Litschke

Kapitalwerte können auch leicht mit wissenschaftlichen Taschenrechnern berechnet werden, z. B. wenn die Ein- und Auszahlungen konstant sind. In allgemeiner Form gilt:

In dieser Formel ist auch eine sofortige Ausgabe oder Investition enthalten, da:

gilt für eine sofortige Zahlungen zum Zeitpunkt t=0:

Titelbild: generiert mit DALL-E von OpenAI